bigO記法について

アルゴリズムを勉強し始めて、まず理解に苦しむ概念。。
自分なりの解釈をまとめてみます。
bigO記法とは
結論、アルゴリズムの性能を一律にわかりやすく記述するための表記である。
アルゴリズムの性能はどのように評価すれば良いのか?
かかった時間だけで評価するのは困難である。
ただ同じアルゴリズムであっても、実行環境やハードが違えば全く異なる結果になってしまう。
そこで一律にアルゴリズムの性能を評価するための指標として計算量という指標が用いられる。
bigOとはその計算量の一般的な記述手法のことである。
実行されるアルゴリズムが、どれほどの時間、記憶領域を使用するかを評価する基準として用いられている。
代表的なオーダー
| 表記 | 意味 | 例 | 早い順 |
|---|---|---|---|
| O(1) | 定数 | 配列の中にアクセスする(ex. a[0] = 1) | 1 |
| O(log(n)) | 対数 | 二分探索:半分ずつ消去法 | 2 |
| O(n) | 一時 | 線形探索:端から順番に見ていく | 3 |
| O(n log n) | n log n | クイックソート:配列をソートしていく | 4 |
| O(n^2) | 二次 | バブルソート:隣り合う要素の大小比較と並べ替えを繰り返す | 5 |
下記にそれぞれの詳細について記述する。
O(1)
O(1)はデータ量がどんなに増えても、常に一回しか処理を行わないことを指す。
function log(arr) {
console.log(array[0]);
console.log(array[1]);
}
log([1, 2, 3, 4]);
log([1, 2, 3, 4, 5, 6, 7, 8, 9, 10]);上記例だと、配列の要素に直接アクセスしている。
データ量が1つだろうが100万だろうが、常にarrayの[0]と[1]番目だけアクセスしています。
一番高速で、データ量が増えても計算量は一定である。
O(log(n))
これはデータ量に対して、計算量が半分になっていく。
function binarySearch(array, key) {
var low = 0;
var high = array.length - 1;
var mid;
var element;
while (low <= high) {
mid = Math.floor((low + high) / 2, 10);
element = array[mid];
if (element < key) {
low = mid + 1;
} else if (element > key) {
high = mid - 1;
} else {
return mid;
}
}
return -1;
}
console.log(binarySearch([1, 2, 3, 4, 5, 6], 3));上記例は二分探索。
処理の回数が少なく、処理時間の観点ではO(1)についで早くなる。
O(n)
これはデータ量(n)が増えただけ、計算量も増える。
計算量はデータ数に比例していく。
function logAll(array) {
for (let i = 0; i < array.length; i++) {
console.log(array[i]);
}
}
logAll([1, 2, 3, 4, 5]);
logAll([1, 2, 3, 4, 5, 6]);
logAll([1, 2, 3, 4, 5, 6, 7]);O(n^2)
「^」ってのは累乗するって意味。(2乗とか)
function addAndLog(array) {
for (let i = 0; i < array.length; i++) {
for (let j = 0; j < array.length; j++) {
console.log(array[i] + array[j]);
}
}
}
addAndLog(["A", "B", "C"]); // 9つの組み合わせ
addAndLog(["A", "B", "C", "D"]); // 16の組み合わせ
addAndLog(["A", "B", "C", "D", "E"]); // 25の組み合わせ上記サンプルは、2乗のループ処理。
計算量は 外側ループのarray長さ * 内側ループのarray長さ。
3*3 = 9でまだいいとしても 5 * 5になると一気に25まで増える。
計算量は指数関数的に増えていくため、アルゴリズムとしてはできる限り避けたいものにはなる。
まとめ
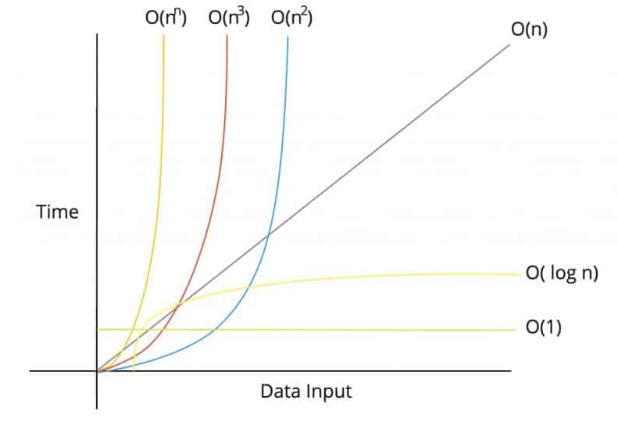
上記は計算量と処理時間の相関関係を示したグラフ。
bigOを意識できるかで、プログラムを見る目が全然違ってくる。
最悪O(n)を超えないように、プログラムを書いていけば、まずは大丈夫だと思う。
良いアルゴリズムとは、問題の規模が大きくなっても対応できるということ。
ただコードを書くのではなく、その中身の性能まで意識してコーディングできるようなエンジニアを目指していきたい。。
